快速上手

基本概念

为了使用 RQFactor ，您需要了解几个常用名词，后文中将直接使用这些名词代指相应的概念。

在股票投资中，我们会经常使用某种指标或者多种指标来对股票池进行筛选，这些用于选股的指标一般被称为因子。在米筐提供的因子系统中，目前仅支持日频率的因子。具体来说，一个因子在其定义的股票池中，对于池中的上市股票，每个交易日每只股票只会计算出一个值。

因子可分为基础因子和复合因子两种：

基础因子：不依赖于其他因子的因子。如基本的行情因子、财务因子，这些因子的值直接来源于财务报表或交易所行情数据；
复合因子：基础因子经过各种变换、组合之后得到的因子（通过"算子"组合生成）。
复合因子又可以分为两种：
- 横截面因子：典型的比如沪深 300 成分股根据当前的 pe_ratio 的值大小进行排序，序号作为因子值。在这种情况下，一个股票的因子值不再只取决于股票本身，而是与整个股票池中所有其他股票有关；对于横截面因子，一个给定的股票在不同的股票池中计算得到的因子值一般是不同的；
- 非横截面因子：仅依赖单只标的自身的历史数据计算，与其他标的无关。例如：单只股票的 5 日均线（MA(close,5)）、10 日涨跌幅（PCT_CHANGE(close,10)），同一股票在不同股票池中，因子值保持一致

对一个或多个因子进行组合、变换，生成新的复合因子，这样的函数我们称为算子，除内置的操作符（如+, -, *, /）外，还可实现时间序列计算（如 MA 移动平均，用于生成日均线因子）、横截面调整（如 RANK 排名，用于生成股票池内因子排序结果）。

在因子开发与应用中，需通过因子检验验证因子有效性 —— 即判断因子是否具备 “稳定预测股票未来收益” 的能力，避免因 “偶然有效” 的因子导致策略实盘亏损。RQFactor 中因子检验的核心逻辑默认 “T 日因子值对应 T+1 日股票收益” 的时间匹配规则（避免未来函数），通过量化指标评估因子与收益的关联度，其中IC值（信息系数） 为因子值与股票下期收益率的相关系数，绝对值越大表示因子预测能力越强。

基于以上概念，如下展示了简单的因子计算、自定义收益率处理及检验全流程，帮助您快速理解RQFactor的使用。

TIP

编写前，用户需导入米筐因子的相关信息

python

from rqfactor import *

一个简单的因子

米筐提供的内置因子可以用 Factor(factor_name) 来引用，如 Factor('open') 表示开盘价这个因子。

python

In[]:
from rqfactor import *
f = (Factor('close') - Factor('open')) / (Factor('high') - Factor('low'))
f

Out[]:
divide(subtract(Factor('close'), Factor('open')), subtract(Factor('high'), Factor('low')))

在上面的代码中，我们定义了一个简单的因子f，它表示股票当天的收盘价与开盘价的差和最高价与最低价差的比值；显然f是一个非横截面类型的复合因子。我们来看看这个因子的依赖：

python

In[]:
f.dependencies

Out[]:
[Factor('close'), Factor('open'), Factor('high'), Factor('low')]

这个因子具体应该如何计算？

python

In[]:
f.expr

Out[]:
(<ufunc 'true_divide'>,
 ((<ufunc 'subtract'>, (Factor('close'), Factor('open'))),
  (<ufunc 'subtract'>, (Factor('high'), Factor('low')))))

expr属性返回了一个前缀表达式树；因子计算引擎正是根据这棵树来计算因子值的。

我们来计算一下平安银行（000001.XSHE）和浦发银行（600000.XSHG）在20180101-20180201的f因子值。

python

In[]:
execute_factor(f, ['000001.XSHE', '600000.XSHG'], '20180101', '20180201')

Out[]:
           000001.XSHE  600000.XSHG
2018-01-02     0.573771     0.647028
2018-01-03    -0.606060    -0.499971
2018-01-04    -0.291667    -0.363636
2018-01-05     0.450003     0.222222
2018-01-08    -0.674419    -0.125000
2018-01-09     0.428570     0.250000
2018-01-10     0.754386     0.780492
2018-01-11    -0.031249    -0.058824
2018-01-12     0.370370    -0.600000
2018-01-15     0.831325     0.608696
2018-01-16     0.083334    -0.250000
2018-01-17    -0.166667     0.358485
2018-01-18     0.727272     0.499980
2018-01-19     0.000000    -0.209317
2018-01-22    -0.313726    -0.363630
2018-01-23     0.508772     0.625013
2018-01-24    -0.034483     0.540540
2018-01-25    -0.531916     0.274994
2018-01-26    -0.406249    -0.666667
2018-01-29    -0.476924    -0.095238
2018-01-30    -0.172413    -0.850003
2018-01-31     0.865385     0.571429
2018-02-01     0.173914     0.410269

execute_factor 会调用因子计算引擎来计算因子值。

算子

在前面的因子定义中，Factor('close') - Factor('open')中减法是怎么回事呢？从业务层面看，非常简单，两个因子相减，生成了一个新的因子；从实现层面看，两个LeafFactor相减？我们来检验一下：

python

In[]:
Factor('close') - Factor('open')

Out[]:
subtract(Factor('close'), Factor('open'))

在上面的例子中，-（减号）正是我们预先定义的一个算子。这个算子对应的是numpy.ufunc.subtract；这个函数由因子计算引擎在计算因子值时调用。

在本系统中，算子除 +, -, *, /, **, //, <, >, >=, <=, &, |, ~, !=这些内置的操作符外，都以全大写命名，如MIN, MA, STD。

与复合因子类似，算子可以分为两类，横截面算子和非横截面算子。一个因子，如果在表达式中使用了横截面算子，就成为了一个横截面因子。一般情况下，横截面因子命名以 CS_ (cross sectional)为前缀，如 CS_ZSCORE；非横截面算子一般不带前缀，或以 TS_ (time series)为前缀，以和类似功能的横截面因子区分。

非横截面算子封装的函数，其输入是一个或多个一维的numpy.ndarray; 横截面算子封装的函数，其输入则是一个或多个pandas.DataFrame。

系统提供的算子可以参考RQFactor API 手册中关于算子的描述

基础因子检验示例

下面几个简单示例覆盖 “基础因子计算→自定义收益率处理→因子检验分析”，帮助您快速掌握从 “因子创建” 到 “有效性验证” 的落地操作：

计算基础因子

基于沪深 300 股票池，计算 20210101 - 20211101 的 pe 因子

python

import pandas as pd
import datetime
from rqfactor import *
import rqdatac
rqdatac.init()
d1 = '20210101'
d2 = '20211101'
f = Factor('pe_ratio_ttm')
ids = rqdatac.index_components('000300.XSHG',d1)
df = execute_factor(f,ids,d1,d2)

计算自定义收益率

将每日 14:00 的分钟 close 数据合成为新的收益率数据

python

price = rqdatac.get_price(ids,d1,d2,frequency='1m',fields='close',expect_df=False)
target = datetime.time(14, 0)
mask = price.index.get_level_values('datetime').time == target
returns = price[mask].pct_change()
returns.index = pd.DatetimeIndex(returns.index.date)

因子检验

构建管道，并将因子值和收益率传入分析器中进行计算

python

# 构建检验管道
engine = FactorAnalysisEngine()
# 添加极值处理
engine.append(('winzorization-mad', Winzorization(method='mad')))
# 添加IC分析器（计算RankIC，按申万一级行业分类，查看行业IC分布）
engine.append(('rank_ic_analysis', ICAnalysis(rank_ic=True, industry_classification='sws')))
# 执行检验
result = engine.analysis(df, returns, ascending=True, periods=1, keep_preprocess_result=True)
result['rank_ic_analysis'].summary()

# Out:
#               P_1
# mean	        0.007487
# std	        0.243561
# positive	  100.000000
# negative	  99.000000
# significance	0.628141
# sig_positive	0.301508
# sig_negative	0.316583
# t_stat  	0.433625
# p_value	  0.665033
# skew	        0.067769
# kurtosis  	-0.774880
# ir	        0.030739

完成检验管道构建后，需调用engine.analysis()执行最终检验，该函数的参数与前文计算的因子值、收益率严格匹配，确保检验结果的准确性。

python

engine.analysis(df, returns, ascending=True, periods=1, keep_preprocess_result=True)

参数

参数名	说明
df	为前文计算的沪深 300 股票池 PE 因子值，要求为 DataFrame 格式且索引、列名与收益率数据一致列
returns	本例中基于 14:00 分钟线构建的自定义日度收益率，需与因子的时间范围、股票池完全对应，避免因数据错位导致的检验偏差
ascending	True 表示因子按升序排序，适配 PE-TTM 因子 “低估值更优” 的价值投资逻辑，若为动量类因子（如股价涨幅），则需设为False
periods	periods = 1 代表调仓周期为 1 个交易日，与日度收益率周期匹配
keep_preprocess_result	True 用于保留极值处理后的因子值，便于后续查看 MAD 法的处理效果，若仅需最终检验结果，也可设为False以减少内存占用

绘制 IC 结果图

python

result['rank_ic_analysis'].show()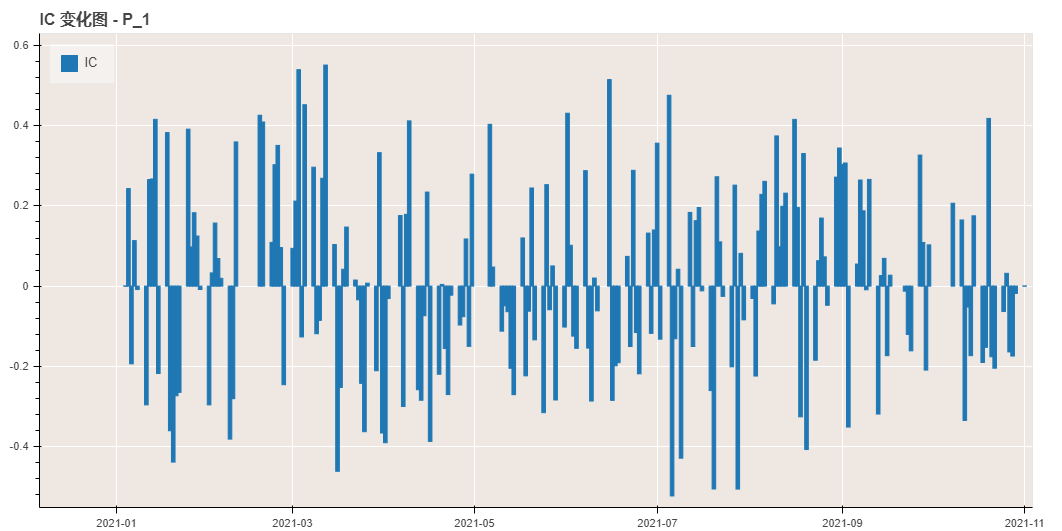

ic结果

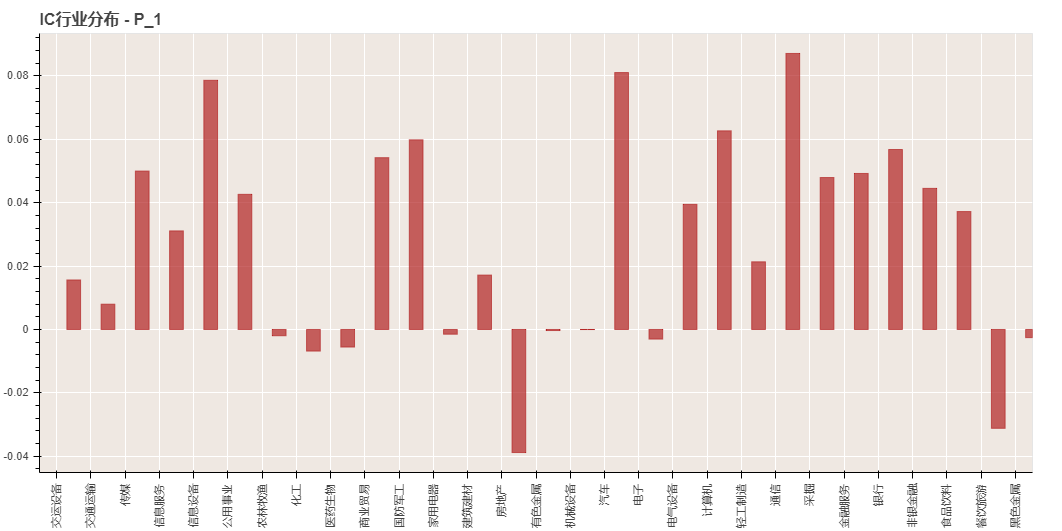
ic行业分布结果

通过上述实战示例，您已掌握 RQFactor 最核心的基础用法。若您需要进一步深入学习，例如开发自定义算子（如特殊均线算法、个性化行业分类），可在后续进阶理解章节中详细了解；更多实战示例可在使用示例中进行参考。若需查询所有 API 的详细参数、算子的完整列表，可参考 RQFactor API 手册，获取更全面的技术支持。

快速上手 ​

基本概念 ​

一个简单的因子 ​

算子 ​

基础因子检验示例 ​

计算基础因子 ​

计算自定义收益率 ​

因子检验 ​

参数 ​

快速上手

基本概念

一个简单的因子

算子

基础因子检验示例

计算基础因子

计算自定义收益率

因子检验

参数